When running in the rain, I often find myself contemplating the fact that a water molecule falling on to my head may have been flowing down a waterfall in the Andes or evaporating off a Patagonian glacier not long before, and centuries before that may have been in Julius Caesar's bladder or on the sweaty brow of Pheidippides as he ran from Marathon to Athens (both of which are less unlikely than you might think, given the number, size and recycling patterns of such particles).

We runners mostly report how much we enjoy the cooling, stimulating effect of light rain. We even pour water over our heads at water stations, so one thing we are not worried about is sheltering from the rain.

On the other hand, there are some runners, but not all, who claim to have a life outside running, a life in which they may be dressed up on their way to a party or to work, only to get caught sans parapluie in a downpour. The obvious way to reach shelter quickly would be to run, not walk, but would it also be the driest way?

​

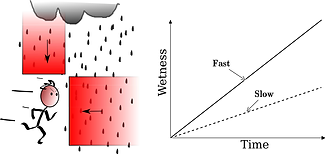
Take these two girls walking in the rain in their stiletto heels, for instance. They will take longer to reach shelter than the girl who has taken hers off in order to be able to run more efficiently - but would the walkers actually be any wetter as a result of lingering longer in the rain?

Most people's behaviour reflects the intuition that running towards shelter is the better strategy for keeping dry. It's just common sense, isn't it? If you are out there for longer, the rain is pouring down on you for longer, so you will get wetter......won't you?

It ain't necessarily so. Leaving aside for the moment the question of what wetness actually means, it turns out that the physics of speeding through rain is rather more complicated that it might at first seem. Our intuitive conviction that we would stay drier if we run has been analysed by scientists using both mathematical principles and rain machine experiments.
So what conclusion do they all come to? Surprisingly, they don't all agree. In part, this reflects their varying assumptions about the initial conditions, but their answer is mostly 'it depends'.....but on what?

Well, as we shall see, speed is indeed a factor for all of them, but for some it also depends on your body shape, on the speed and direction of the wind relative to your direction of movement, and on rain droplet size. And in some circumstances, running too fast can make you wetter, they say.

Oh, and it matters whether you are bald or not. And whether you have an umbrella.
 

The real world dynamics and non-linear variables are so complex here that, for simplicity's sake and for easier illustration of the fundamental problem, physicists mostly assume that the rain and wind remain constant during any particular trip from a rainy A to shelter at B, but a first step in any analysis requires a clear statement of the phenomenon being investigated, so let's strip it down to the essentials.

Let's assume that we have a regular cuboid body (i.e., a stretched cube shape, like a 3D oblong) moving through falling droplets of water as it moves from A to B. For now, we will directly link the quality known as 'wetness' with the number of droplets that make impact on that body's surface. The goal is to find out how changing the body's speed between A and B affects the number of droplet impacts, and hence the wetness.

The simplest situation is vertical rain falling on a stationary body. The number of drops falling on to that body will then obviously depend on how long it falls for (although there will be more on a wider person, of course).

Once the body starts moving, there is still the same amount of rain falling vertically on to it as when it was still, but it is now moving into a 'box' and bumping into additional droplets in front of it, so it will get even wetter once it starts moving through the vertical rain (see below).
 

But what happens if you speed the body up? This would not affect the amount of constant vertical rain falling per second on top of it, but, since it would reach shelter at B quicker, there will be fewer seconds under the rain, and hence fewer vertical droplet impacts, and hence less wetness. The vertical contribution to the wetness of the body is thus reduced by increased speed, which has reduced the time spent under the deluge. This is in accord with our common sense notion - run to keep dry.

However, a faster forwards movement will surely bump into more droplets per second in the 'box' in front of it (albeit for a shorter number of seconds) until it reaches shelter at B, so what does this mean for the frontal, horizontal contribution to wetness?

Assuming that the rain droplets are evenly distributed and falling vertically at a constant rate, at each instant of time there will be the same number of droplets in the 'box' you are running through from A to B - rain enters and leaves the 'box' at the same rate. As the video clip below explains, it then becomes analogous to a snowplough going through a given amount of snow - however fast the plough goes, it will always impact on the same amount of snow at each instant of time.

The size of the box is fixed, and the number of droplets impacting on you is both fixed and equal at each stage of your progress, so adding up those impacts from each moment will must give you the same number whether you go fast or slowly. The impacts per second and the total number of seconds will be different at different speeds, but the total number of impacts will not be.

Put simpler, if you run fast, you will go through more droplets per second, but for fewer seconds, whereas if you walk slowly, you will hit fewer droplets per second, but for longer. So, your speed makes no difference to the horizontal contribution to wetness.

Overall then, from these two contributions, it would seem that it's worth running in vertical rain, i.e., when there's no wind.

This is brilliantly but rather breathlessly explained in this short clip from MinutePhysics:

https://www.youtube.com/watch?v=3MqYE2UuN24

However, any analysis of a real world situation must depend on the accuracy of the model that you are using to represent that situation - you play around with the model according to certain rules, and then map any discoveries back on to the real world, where conclusions can be drawn.

In this case, there is a need for practical purposes to simplify the model, the variables and the assumptions about initial conditions, and we know from chaos theory how sensitive the outcomes can be to initial conditions (the 'butterfly effect'), how tiny changes or errors can be amplified.

For instance, a bigger size of raindrop means a faster rate of descent, assuming they all have similar densities, and this will affect the impact rate, but scientists must assume an average size, again for practical reasons.

Similarly, the cuboid shape does not accurately reflect the irregular shape of the human body - actually, most analysts use a parallelipiped, which leans more like a runner - and the speed and direction of a gusting wind are anything but constant, so we have so far really only been looking bluntly here at a kind of average interaction between precipitation and moving humans.

For those of a mathematical bent, here is an illustration of the difference between the complicated, more accurate situation and the simplified, more practical version. The first equation describes the rate at which you get wet, but it includes surface area, which is almost impossibly difficult to calculate in practice in an irregular shape. (W is wetness, V is velocity, dt is unit time, dA is unit surface area, P refers to the person, R to the rain, and ρ is rain density, i.e., the amount of water per unit volume).

​

And here's the equation after simplifying the situation, where W is total wetness over distance D to the shelter, a is the top surface area and A is now the front surface area:

Despite the approximate values we use for those real world factors which vary from moment to moment and refuse to remain as constant or regular as we'd like them to be, the calculus in the top equation is a powerful mathematical tool in the analysis of what is happening in each instant of time. It can then get the overall picture by integrating its results over the total time taken (see more in 'This is "motion towards", isn't it, boy?').

Other equations confirm that the frontal impact of vertical rain is independent of one's speed through it, while the vertical component of the rain falling on top of you depends on it. So, overall, the theory would appear to show that it's prudent to run if you want to keep dry.

But here's the rub: we are generally clothed when out in the rain, and so fabric absorbency and its retention of water comes into play. After all, if our clothes are sodden, we say we are wet through.

Intriguingly, an experiment carried out by the US TV show 'Mythbusters' claims that the science is wrong: your clothes, and by extension you, will be drier overall if you WALK in the rain, although it has also been criticised for not taking into account many other pertinent factors (including the way runners' thighs are more horizontal than those of walkers.....and the amount of hair on the head, which can act as a sponge retaining water until it becomes so saturated that its load is released to flow down on to the rest of you): https://www.youtube.com/watch?v=HtbJbi6Sswg

Back with the theoreticians, their calculations show that if there is a reasonable tailwind, it is better to run at the same speed as the wind, and no faster. You will then outrun the droplets behind you and yet be slow enough not to collide with many droplets falling away from you in front. (In the top equation, the bracket would be zero, so the increase in wetness due to the tailwind would also be zero, although the vertical rain will still soak you, of course.)

A headwind, however, requires that you run as fast as you can. Using the snowplough analogy above, it is as if the snow is moving towards you, with more coming into the 'box' from the far end than can leave (as the exit is blocked by the snowplough) - you would have to move more snow over the same distance, and more snow per second, but the faster you do it, the less snow you will have to move.

Similarly, back in the rain, the droplets per second coming into the 'box' from the far end are not the same as those leaving it, as the exit for the rain in the 'box' is blocked by you, so you will encounter more of them per second, and so the fewer seconds you take to cover the distance, the fewer total number of impacts you'll have, and the less wet you'll become.

​

As for wetness, scientists at Loughborough University have found that, although we do not have specific skin receptors for wetness, the way we sense temperature, pressure and texture relates a particular combination of them to our previous experience of water, sweat, etc..

It is thus more of a perception than a true sensation, and hairier people are more, not less, sensitive in perceiving wetness precisely because it is not sensed through the skin, and also because hairs can transmit information, especially pressure.

Runners, of course, have fewer items of clothing to get wet (and often less hair). The clothing is designed to be light even when wet, and it promotes easier evaporation. In any case, you can only get so wet.

So, to conclude: if the rain is more or less falling straight down or is borne in a headwind, running and not walking towards shelter will keep you drier. If the wind is blowing the rain at you from behind, try and run or walk at that same speed (and good luck with assessing what that is!).

As for rain and the runner, well, we embrace the elements. After all, rain is the most dramatic aspect of the continuous exchange of water between the earth's atmosphere, its ground and its plants. The next time it refreshes my run, it may even contain some of the very particles that I had sweated out years before during my first hot and hilly marathon. Or they may have been in my blood or in my brain. Or even in my carbo gel.

I welcome them back.

​

B/w photograph of the UK's Cumbrian Lake District by John Gravett/Cavendish Press